| Oceans are critical to proving that humans are having an impact on the climate.
The big scary number of the week is 15 × 1022 (or 150 million quadrillion). It’s the number of Joules the ocean has apparently heated by since 1961. But convert it to degrees per year and suddenly the big scary 15 × 1022 becomes three thousands of one degree per year. Unmeasurably small. So realists everywhere, lets check the math, and get ready to spread the word. Everywhere you see the ocean heat capacity argument or graph, let people know the numbers just don’t add up. THIS POST HAS BEEN UPDATED SEE HERE FOR THE LATEST FIGURES. … |
|
The developing Bumper Sticker Message to cut and paste is:
15 × 1022 Joules since 1961 = 3 thousandths of a degree warmer per year. Who cares?
… Below Michael Hammer goes through the calculations he started on the comments thread for “Ocean temperatures: The new bluff in alarmism.” Essentially he confirms Kininmonths numbers and calculates:
Yes the numbers below are not easy reading, but this is worth sorting out. This is a joint posting with Jennifer Marohasy, so for those interested in her view and more analysis check there too. Thanks to Michael for his dedication in doing the maths. I will update the numbers if we make any further advances in calculations so check back here. If CO2 is warming our planet, why can’t we find the heat? Cheers! JoNova |
A Climate Change Paradox
Guest Post By Michael Hammer
AUSTRALIA’S Minister for Climate Change, Penny Wong, recently suggested that most of the global warming since 1960, about 85 percent, has happened in the oceans and that change in ocean heat content is thus the most appropriate measure of global warming.
But, calculating from first principles, according to this data the oceans have absorbed far less energy than the IPCC estimates for the impact of rising carbon dioxide levels. While the government data suggests a warming rate of 0.38 watts/ m2 the IPCC data suggests a warming rate of 3.6 watts/ m2. This is a significant discrepancy of nearly 10:1 3:1 and needs to be resolved. If the oceans really are the major heat sink for the planet where is the rest of the energy going? Alternatively, is the error in the IPCC estimates.
THIS POST HAS BEEN UPDATED SEE HERE FOR THE LATEST FIGURES.
Here’s my logic:
On June 24, 2009, the Minister for Climate Change posted a ‘Response to Senator Fielding’s questions about the climate change science’.
This article included the above graph and comments reproduced below. The straight red line on the ocean heat content graph, however, is my addition and was not part of the original article. The line was placed by eye and is not claimed to be a least squares line of best fit.
The quoted items below are taken from the Minister’s website.
“In terms of the climate system as a whole, only about five percent of the warming since 1960 has taken place in the air.”
“Most of warming since 1960 (about 85 percent) has happened in the oceans. Thus, in terms of a single indicator of global warming, change in ocean heat content is the most appropriate.”
“The change in ocean heat content since 1960 is shown in the figure below. Note the significant warming trend since 1998.”
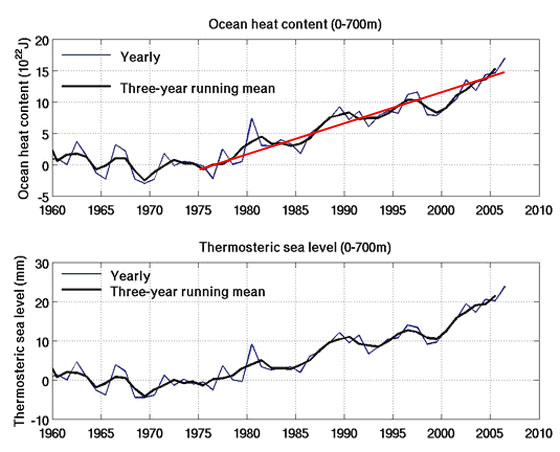
I note that the graph is labeled ocean heat content which cannot be correct given that the value is shown as zero prior to 1975. However the text suggests it is actually change in ocean heat content which would seem reasonable. I have assumed that to be the case.
The graph shows that over the last 30 years the oceans have absorbed 15×1022 joules of energy and as the red line shows this has been very close to linear over that time. Using a linear approximation implies the oceans have absorbed about 15×1022 / 30 or 5 × 1021 joules per year.
How does this compare with the claimed degree of global warming from rising carbon dioxide – expressed in watts / m2. Convert ocean warming first to watts = joules per second. There are 60 × 60 × 24 × 365 seconds per year = 3.15 × 107 seconds per year. So the oceans are absorbing 5 × 1021 / 3.15 × 107 joules per second = 1.6 × 1014 watts.
Now to get watts / m2 we need to divide the watts by the surface area of Earth. The Earth is a sphere of radius 3960 miles = 6336 km. Its surface area = 4 × pi × radius2 = 5 × 108 sq km (Wikipedia quotes 5.1 × 108 sq km). Since there are 106 m2 per km2 this equates to 5 × 1014 m2. Thus the oceans are absorbing energy at the rate of 1.6 × 1014 / 5 × 1014 watts/ m2 which equals 0.32 watts/ m2.
The article states that 85 percent of the warming has taken place in the oceans which would seem to be saying that 85 percent of the retained heat due to AGW is being stored in the oceans. From this it follows that the total retained heat is 0.32/0.85 or 0.38 watts/ m2.
The Intergovernmental Panel on Climate Change in their 4th assessment report (summary for policy makers) claim (page 12, 4th bullet point) that “…..global average surface warming following a doubling of carbon dioxide concentrations. It is likely to be in the range 2 to 4.5°C with a best estimate of about 3°C”.
Now to get a 3°C rise at the average claimed emission temperature (255K) requires an additional energy input (additional energy retained by greenhouse gases) of 11.3 watts/ m2. This assumes the 3°C is an equilibrium level. If it is not then the retained energy must be still higher so the 11.3 is a minimum figure.
The ocean heat graph from the Minister ends in 2006. According to Mauna Loa data in 2006 the carbon dioxide concentration was 383 ppm which represents 0.45 doublings and hence an increase in global warming retained energy of 11.3 × 0.45 = 5.1 watts/ m2. Not all of this represents energy absorbed by the planet because of the claim that the planet has warmed. This warming will increase the energy radiated back out to space.
The Climate Research Unit at the University of East Anglia shows the claimed warming in 2006 was 0.4°C. SkepticalScience.com shows temperature rise graphs from three sources and all show about 0.4°C temperature rise in 2006. Using the same claimed effective emission temperature as above (255K), a rise of 0.4°C will increase emitted energy by 1.5 watts/ m2. Thus the net additional energy retained by Earth will be 5.1 – 1.5 = 3.6 watts/ m2.
This presents a considerable conflict. Ocean heat assessment suggests earth is gaining energy at the rate of 0.38 watts/ m2 while carbon dioxide analysis suggests the rate is 3.6 watts/ m2. This is a difference of nearly 10:1 in two different analyses of the same quantity. Both cannot be right.
I note that the Minister specifically draws attention to the “significant warming trend since 1998”. This could be taken to mean a claim that the linear slope does not apply.
This is a somewhat risky assumption since there are other periods where the slope is well above the slope of the red line. None the less, using the local slope over the years since 1998 corresponds to about 8.8 × 1021 instead of the average of 5 × 1021. That would make the retained heat in the oceans about 0.56 watts/ m2 for a total retained heat of 0.66 watts/ m2. This is still 5.5 times lower than IPCC claim for the impact of carbon dioxide. Also, if we accept the higher slope since 1998 it means the average ocean energy absorption over the earlier years is reduced to 8 × 1022 joules over 23 years corresponding to 0.22 watts / m2. Since the carbon dioxide concentration from the Mauna Loa data in 1998 was 366.6 ppm this represents 0.39 doublings equivalent to an additional 4.4 watts / m2 or about 3 watts/ m2 after allowing for temperature rise making the discrepancy over those years worse (3 vs 0.22 is a ratio of 13.6:1).
What the Minister’s own data shows is that the oceans have only absorbed between about 9 and 14 percent of the excess anthropogenic global warming energy implied by IPCC data. Yet they claim the ocean absorption represents 85 percent of this energy. The oceans are by far the biggest heat sink on the planet. If they are only absorbing at most 14 percent of the excess energy it is extremely difficult to see where the rest of the energy could be going.
Could the error be in the ocean heat content – maybe the exponent should be 23 not 22? Oceans cover 70 percent of the Earth’s surface or 3.5 ×1014 m2. If the energy is spread over the top 700 m as the graph caption states, the volume of water is 3.5 × 700 × 1014 = 2.45 × 1017 m3 . Water has a thermal capacity of 4.18 million joules per degree per m3. Hence the 15 × 1022 joules will raise the surface ocean temperature by 15 × 1022 / ( 2.45 × 1017 × 4.18 × 106 ) degrees = 0.15°C (This by the way is exactly the same result as Bill Kinninmonth cited in his email to Professor English). This result assumes the energy is distributed uniformly throughout the 700 meter depth. If it is concentrated near the surface the rise would be higher. To match the IPCC predictions the energy absorption would have to be 5.5 to 10 times higher suggesting an ocean temperature rise of at least 0.8°C to 1.5°C over the last 30 years. No such rise has been reported.
It would seem that the only plausible alternative left is that the error is in the IPCC estimates and that the current value should be about 1.5 + 0.38 = 1.88watts/ m2 (additional energy radiated plus rate of energy storage in the oceans). If so by 2070 the additional energy input over today would be 1.88 × 0.55/0.45 = 2.3 watts / m2. (We have had 0.45 doublings with a further 0.55 to go by 2070).
Such an energy rise at equilibrium would give an additional temperature increase of 0.6°C. This is of course if we assume that the currently claimed temperature rise is correct and is all due to carbon dioxide.
So many assumptions and such a paradox!
Michael Hammer,
Melbourne, Australia
